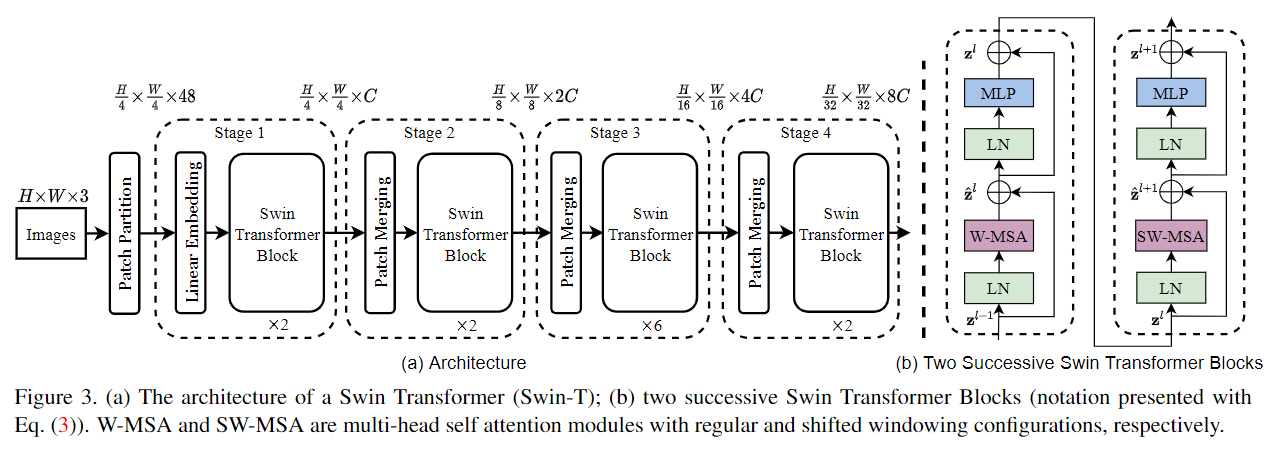
Swin Transformer V1论文笔记

paper

Swin-Transformer-V1网络结构：

不同参数量级的Swin的设置：

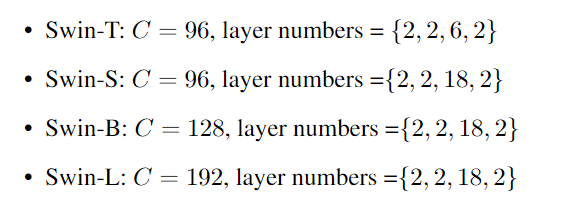
网络结构解读：

1. Patch Partition: 为每一个图片分为不同patch

2. Linear Embedding: 用于Stage 1: 将通道数48映射到任意的C，很像序列attention的第一步：将符号信息->向量

3. Patch merging: 降采样，比如stage2: merging的作法是，将feature map切patch，为[H/8, W/8]，channel维变为4C，[B, H/8, W/8, 4C]再通过一个线性层将4C映射到2C

4. Window partition: 将(B,H,W,C)的图片划分为(num_windows*B, window_size, window_size, C)

5. 	Window Partition	computation skills	context
   W-MSA	regular	–	only window
   Sw-MSA	shifted	cyclic shift	only window
   MSA	regular	–	global

   Layer l - regular partition Layer l+1 - shifted partition

   

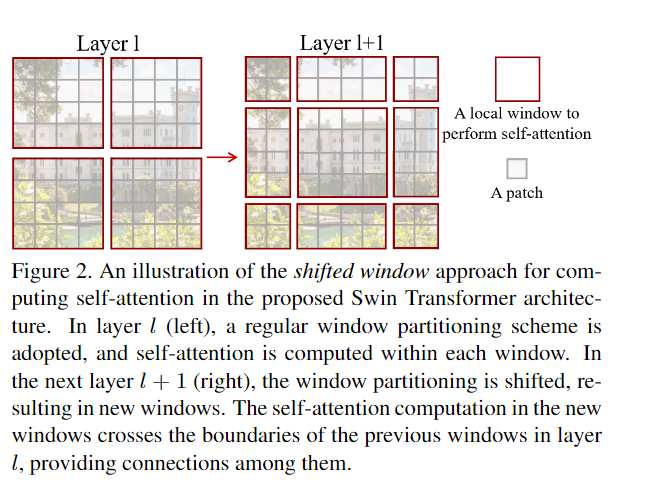
   shifted window Pros 克服了窗口间缺乏connections的弱点

   

   无计算技巧时的shifted window计算量：

   以Figure 2为例：regular计算量是2×2的窗口数。而shifted如果不用cyclic技巧，就需要加Pad，将所有窗口都变为4×4Patch的窗口大小，再计算，所以计算量就是3×3的窗口数，计算量×2.25

   Cyclic shift computation skill: 只用4 windows的计算量，得到9 windows的self-attention结果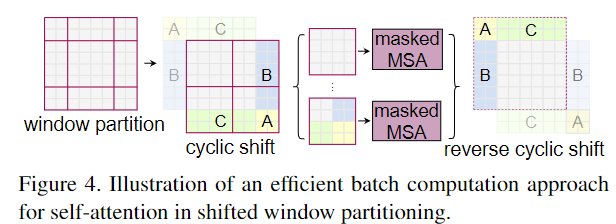

   

   这样的话计算量还是2×2的窗口数，而且加入了窗口间的connection

   masked MSA: 先明确window-based self-attention机制是窗口内部j计算attention，按照shifted window partition的分割方法，例：A模块即使被cyclic shift到图像的下方，也只能和A的转置进行计算attention，不然如果A是天空，灰色部分是地面，shift后A矩阵和灰色部分的矩阵的点乘得到的结果是不合理的，故计算的时候需要mask，负责遮住A与非A部分的矩阵点乘结果。这也符合我们对computation skill的理解，加入了cyclic shift的Sw-MSA与有pad的W-MSA计算的attention结果相同

   reverse cyclic shift: 将A,B,C复位

6. Relative position bias

   1. 修改后的Attention(Q,K,V)

      

      B是[M², M²]大小的矩阵

   2. 给一个Window的不同位置的patch加一个位置编码（reference blog）

      

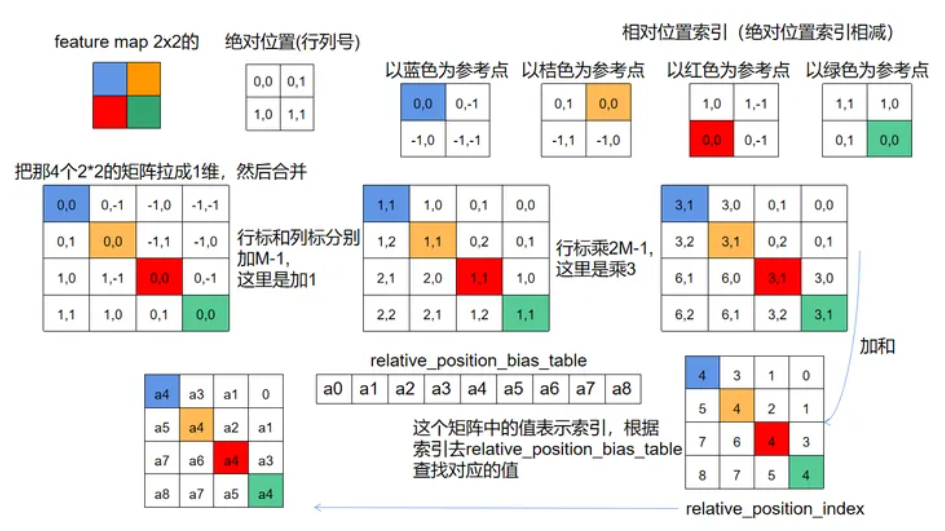
      拉成1维合并后 + M-1 -> 索引非负

      行标×(2M-1) 可以区分开关于主对角线对称的位置，并且对结果加和，区间为[0,8]，这个结果可以作为relative_position_bias_table的索引

      table怎么计算：

      relative_position_bias_table = nn.Parameter(torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1)))
      trunc_normal_(relative_position_bias_table, std=.02) # 正态分布应该是为了控制相对位置编码在(-1, 1)之间，位置编码的原则可以看我Attention is all you need的论文笔记