Transformer
Attention有无限长上下文窗口,之前序列生成算法(LSTM, GPT2)的难点
Query: 类比Google输入框
Key: Google根据Query为你匹配到的关键词
Value: 查询到的网页
Encoder-Decoder结构:
Encoder: 将文本序列变为带有注意力的向量表示
Decoder: 生成序列
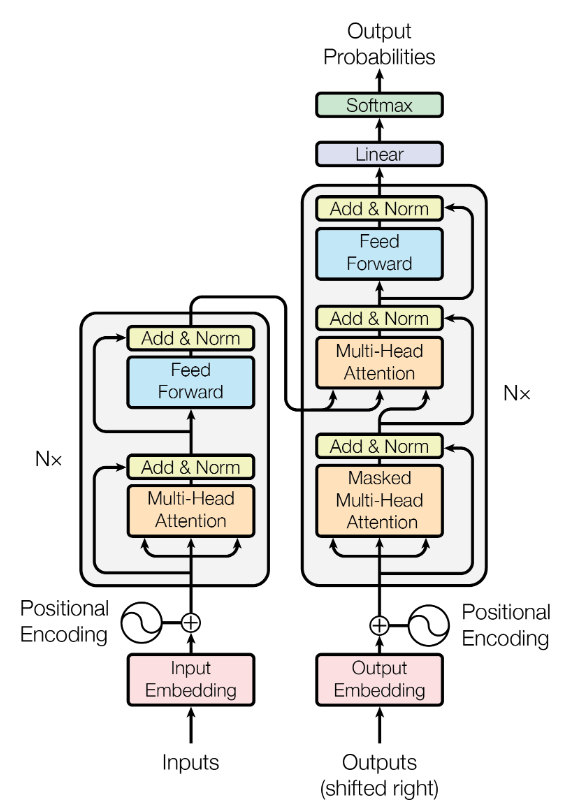
模块化解读
Input Embedding: 输入的symbol representation映射到continuous presentation(向量)
Positional Encoding: 将token的位置信息映射到向量(位置信息对语义的表达很关键)
数学实现:

1)d<=>d
model,和Input Embedding层输出的向量维度相同 i的计算方法由下面的示例说明
2)编码原则:唯一性,不同长度序列的token间间隔含义相同
3)为什么不用index of token作为位置编码:For long sequences, the indices can grow large in magnitude. ==If you normalize the index value to lie between 0 and 1, it can create problems for variable length sequences as they would be normalized differently.==这违背了一个位置编码的原则:对于不同长度的序列,token的间隔的含义要相同 –> 最好编码完,得到的位置信息自然∈(0,1)
4)Example:
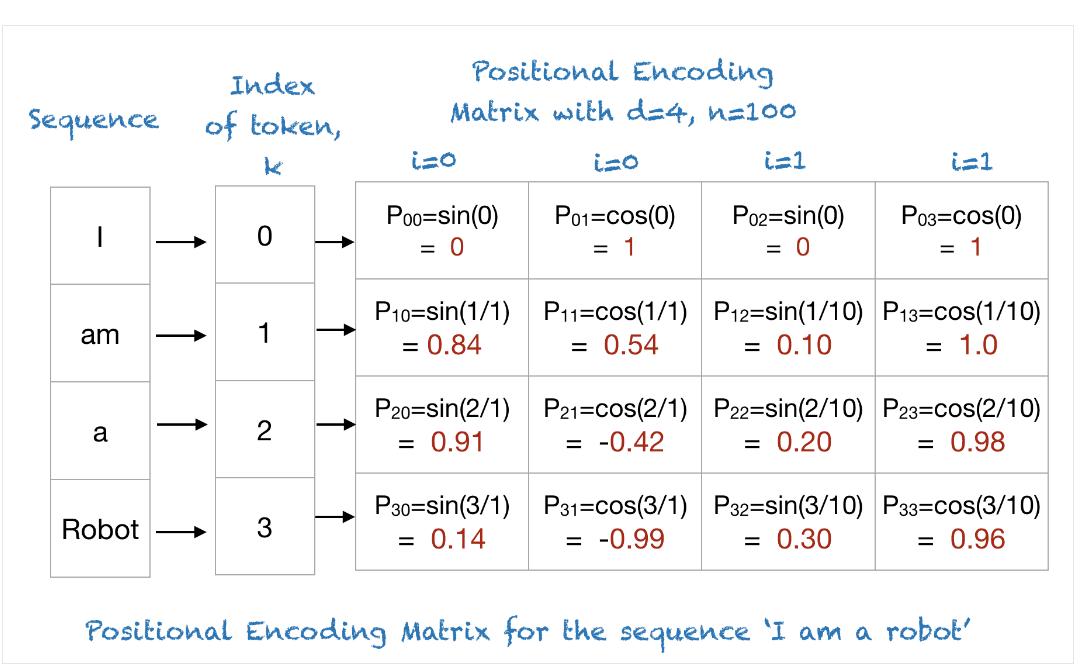
i的计算方法:0≤i<d/2=2,4维的positional encoding的index=0,1,2,3,index为奇数,2i+1=index,index为偶数,2i=index。上图的index对应得出i的取值0,0,1,1
根据示例分析是否符合编码原则:
- 位置编码向量是否唯一:看上图矩阵第一列,编码始终为sin(2i+1)或cos(2i) (i∈N),根据对称性,因为sin和cos对称轴始终不在自然数上,所以不可能有相同的,满足唯一性
- 不同长度的序列,token之间的间隔的含义要相同,因为这种方式产生的编码自然在(0,1)区间,不需要normalization。这里的不同长度序列,它们的(n, i, d)这个三元组取值都相同,只是k的范围不同,那么token的间隔始终相同
Multi-Head Attention:
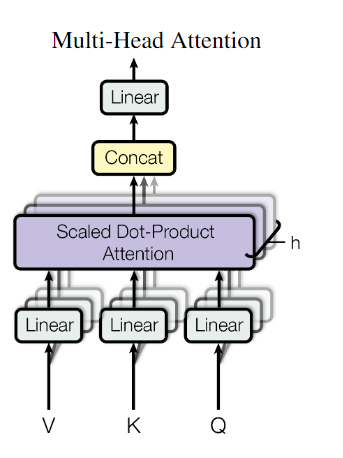
h for “Head” num

Q, K, V都是d
model列W
i是weight矩阵,dmodel= nhead* dk代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52class MultiHeadAttention(nn.Module):
''' Multi-Head Attention module '''
def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1):
super().__init__()
self.n_head = n_head
self.d_k = d_k
self.d_v = d_v
self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False)
self.fc = nn.Linear(n_head * d_v, d_model, bias=False)
self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5)
self.dropout = nn.Dropout(dropout)
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, q, k, v, mask=None):
d_k, d_v, n_head = self.d_k, self.d_v, self.n_head
sz_b, len_q, len_k, len_v = q.size(0), q.size(1), k.size(1), v.size(1)
residual = q
# Pass through the pre-attention projection: b x lq x (n*dv)
# Separate different heads: b x lq x n x dv
q = self.w_qs(q).view(sz_b, len_q, n_head, d_k)
k = self.w_ks(k).view(sz_b, len_k, n_head, d_k)
v = self.w_vs(v).view(sz_b, len_v, n_head, d_v)
# Transpose for attention dot product: b x n x lq x dv
q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2)
if mask is not None:
mask = mask.unsqueeze(1) # For head axis broadcasting.
q, attn = self.attention(q, k, v, mask=mask)
# Transpose to move the head dimension back: b x lq x n x dv
# Combine the last two dimensions to concatenate all the heads together: b x lq x (n*dv)
q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1)
q = self.dropout(self.fc(q))
q += residual
q = self.layer_norm(q)
return q, attn # 返回输出和attentionlen_q, len_k, len_v对应论文中的d
model,并且相等Scaled Dot-Product Attention:
比较Query和Key相似度->softmax->对Value加权
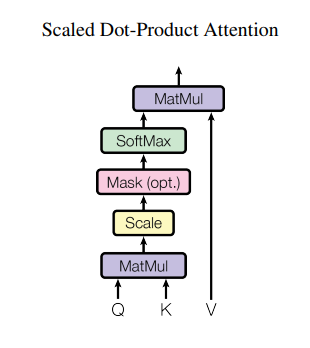
为什么要Scale: 论文原文:We suspect that for large values of d
k, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients- 由于softmax函数计算方法使用了指数函数,如果d
k大了,参与QK^T^点乘的元素个数增加,产生的矩阵,各个位置的值大概率变大,反向传播时,梯度极小 - 指数函数可能存在数值的上溢和下溢问题
Mask矩阵: Mask是一个bool型矩阵。在第 i 时刻做注意力计算时,>i 的时刻都没有结果,只有<i 的时刻有结果。注意力只与之前的内容相关,因此需要做Mask,将QK^T^点乘产生的矩阵中,在Mask规定的需要掩住的位置上,将结果矩阵值设为-1e9,经过softmax后就是0
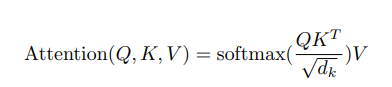
- 由于softmax函数计算方法使用了指数函数,如果d
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class ScaledDotProductAttention(nn.Module):
''' Scaled Dot-Product Attention '''
def __init__(self, temperature, attn_dropout=0.1):
super().__init__()
self.temperature = temperature # 1/sqrt(d_k)
self.dropout = nn.Dropout(attn_dropout)
def forward(self, q, k, v, mask=None):
attn = torch.matmul(q / self.temperature, k.transpose(2, 3))
# mask --> 只能通过现有的output序列生成新的序列
if mask is not None:
attn = attn.masked_fill(mask == 0, -1e9)
attn = self.dropout(F.softmax(attn, dim=-1)) # dropout应该也是option ?
output = torch.matmul(attn, v)
return output, attn
Decoder:
搞清三个输入箭头:
- Outputs(shifted right): 将生成的序列作为输入
- 将Encoder输出的Attention向量作为第二个Multi-Head Attention的Attention
为什么要用Masked Multi-Head Attention
因为这是对生成序列进行Attention,而每一时刻生成的序列,只能与之前生成的序列关联
如何进行mask:
